Akuisisi Citra
Daftar Isi:
- Model Kamera Pinhole
- Model Kamera Thin Lens
- Sensor Array
- Sampling dan Quantization
- Resolusi dari Citra
- Latihan
- Referensi
Akuisisi Citra dikatakan sebagai proses mengubah objek ataupun latar (scene) menjadi ke dalam bentuk digital. Pembahasan pada materi ini dimulai dari model akuisisi citra yang paling sederhana.
Model Kamera Pinhole
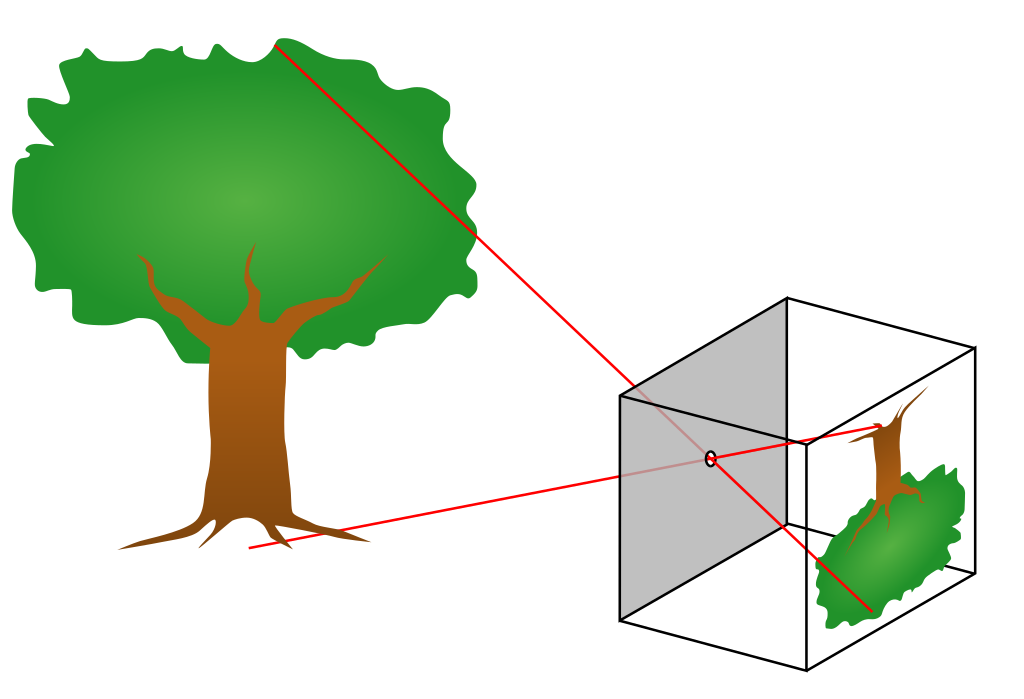
Gambar 2.1. Model kamera pinhole yang memproyeksikan terbalik objek atau latar.
Kamera pinhole merupakan model kamera yang paling sederhana dan telah digunakan sejak abad ke-13 [1]. Saat ini, model ini sudah tidak lagi digunakan. Namun, model ini sangat berguna untuk membantu dalam pemahaman terhadap komponen optik dari kamera.
Kamera pinhole berbentuk kotak seperti kubus atau balok tertutup dengan lubang kecil di salah satu sisi. Lubang ini berfungsi sebagai jalan masuk cahaya yang kemudian akan memproyeksikan objek atau latar menjadi terbalik di sisi dalam yang berlawanan dengan sisi lubang. Perhatikan Gambar 2.1.
Model Kamera Thin Lens
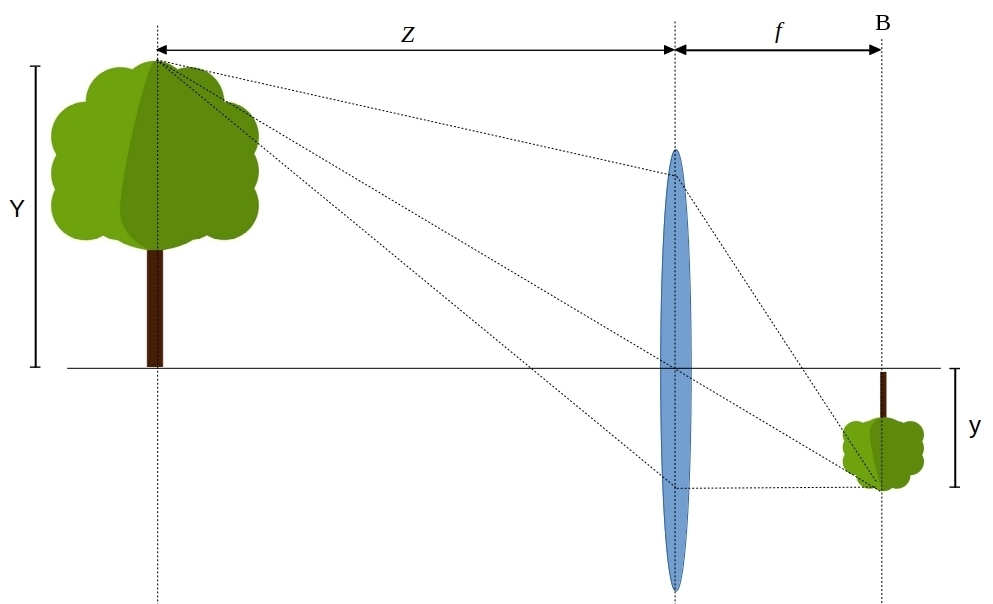
Gambar 2.2. Model kamera Thin Lens. (B) adalah bidang citra
Model kamera pinhole memang sangat memudahkan dalam pemahaman konsep geometri kamera. Namun, model ini tidak pernah dipakai untuk praktik. Hasil proyeksi dari model pinhole tidak terlalu tajam. Kelemahan dari pinhole ini dipecahkan dengan model lensa tipis yang menggantikan posisi lubang jarum.
Masih ingatkan kalian dengan hukum pembiasan cahaya? Perhatikan Gambar 2.2. Sinar datang sejajar dengan sumbu, dibiaskan menuju titik fokus. Sinar datang melalui titik fokus, akan dibiaskan sejajar sumbu utama. Dan yang terakhir, sinar datang melalui pusat optik, tidak mengalami pembiasan.
Sensor Array
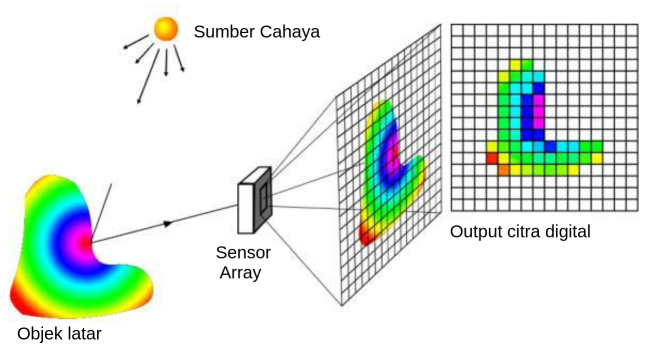
Gambar 2.3. Ilustrasi pencitraan dengan Sensor Array.
Pada Gambar 2.3, objek latar memantulkan cahaya dari sumbernya (contoh: cahaya matahari dan pantulan cahaya dari permukaan objek). Pantulan cahaya ini kemudian ditangkap oleh sensor. Di dalam sensor ini, ada dua proses yang berjalan. Pertama. pemfokusan cahaya oleh lensa terhadap objek ke dalam bidang citra. Kedua, konversi dari data analog ke dalam bentuk digital.
Sampling dan Quantization
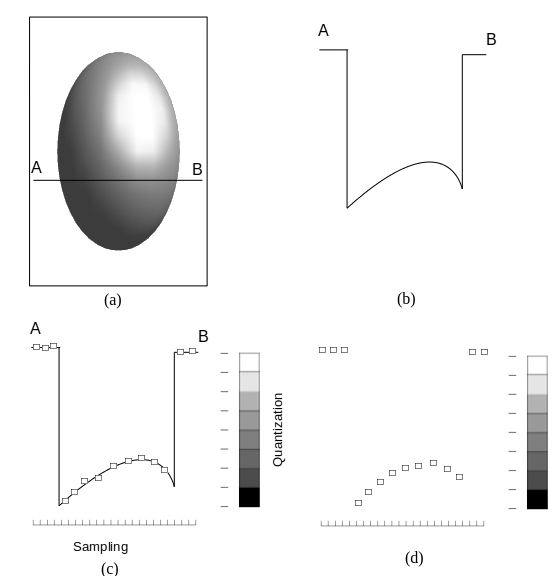
Gambar 2.4. Proses digitalisasi citra.
Pada subbab sebelumnya, kalian sudah mempelajari proses terjadinya akuisisi citra. Tujuan utama dari semua ini adalah mendapatkan citra digital. Demi mendapatkan citra digital, dua proses yang perlu dilalui, yaitu sampling dan quantization (SQ).
Anggap ada sebuah citra kontinyu \(f(x,y)\) yang akan didigitalisasi seperti pada Gambar 2.4 (a) yang memiliki intensitas dan koordinat kontinyu pada \(x\) dan \(y\). Tidak mungkin semua posisi koordinat sumbu \(x\) diubah ke dalam digital karena sifatnya yang kontinyu. Oleh karena itu, diperlukan beberapa sampel posisi dari sumbu \(x\), sumbu \(y\) dan demikian juga untuk intensitas. Digitalisasi tiap sumbu disebut dengan sampling sedangkan pada intensitas disebut dengan quantization [3].
Visualisasi SQ dilakukan sebagaimana Gambar 2.4. Dari citra kontinyu Gambar 2.4 (a), diambil sampel dari satu titik koordinat pada sumbu tertentu yang kemudian diproyeksikan secara vertikal seperti pada Gambar 2.4 (b). Analoginya seperti berikut, bayangkan kalian punya roti tawar yang masih utuh keluar dari oven. Kalian lihat dari atas, seperti itulah Gambar 2.4 (a). Lalu, kalian iris tipis seperti roti tawar pada umumnya, ambil satu bagian. Kemudian angkat dan lihat sisi dalam atau tengahnya, seperti itulah Gambar 2.4 (b).
Dalam sampling, posisi koordinat dibagi menjadi beberapa bagian dengan berdasarkan skala tertentu. Pada kasus ini, citra kontinyu dibagi menjadi 15 titik sampel. Tiap titik direpresentasikan dengan kotak putih kecil seperti pada Gambar 2.4 (c). Demikian pula untuk quantization, intensitas tiap titik dikonversikan 8 skala pada sisi kanan Gambar 2.4 (c). Hasil dari SQ adalah seperti pada Gambar 2.4 (d). Jika dilihat dari sisi atas, maka didapat hasil proyeksi sebagaimana pada Gambar 2.5.
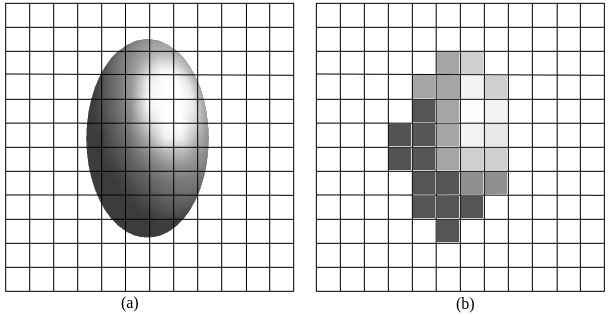
Gambar 2.5. (a) Citra kontinyu diproyeksikan oleh sensor array. (b) Hasil SQ
Sudah nampak jelas bagaimana kualitas citra dipengaruhi oleh kerapatan skala pada sampling dan quantization. Semakin banyak jumlah skala tersebut maka semakin bagus pula kualitas citra yang dihasilkan.
Resolusi dari Citra
Ukuran representatif dari citra digital dinamakan dengan resolusi [4]. Ukuran ini memiliki tiga istilah:
-
Spasial
Resolusi spasial ini diukur dengan lebar x panjang citra. Misalnya: 800 x 600, 1024 x 768, dan seterusnya. Ukuran-ukuran ini berkaitan dengan jumlah sampling. Semakin tinggi resolusi spasial, semakin banyak pula sampling-nya.
-
Temporal
Resolusi ini biasanya dipakai untuk mengukur citra bergerak atau video. Ukuran dari resolusi ini adalah Frame per Second (FPS). Misalnya: 25 fps, 30 fps, 50 fps, dan seterusnya. FPS memiliki arti banyaknya citra yang dihasilkan dari sensor setiap detiknya.
-
Bit
Resolusi bit ini sangat berkaitan erat dengan quantization. Resolusi bit adalah banyaknya intensitas warna yang bisa ditampung dalam satu piksel. Contoh:
-
Citra biner (Binary Image)
Citra yang hanya memiliki nilai intensitas [0,1] atau \(2^1\). Angka 1 pada \(2^1\) adalah bit. Contohnya: citra hasil fax (faximile)
-
Citra Grayscale
Citra dengan 1 kanal yang memiliki nilai intensitas [0…255] atau \(2^8\). Dengan nilai 8-bit per pikselnya, maka citra ini dengan ukuran 800 x 600 piksel memiliki ukuran file sebesar 468,75 KB.
-
Citra RGB (true color image)
Nilai intensitasnya sama dengan citra grayscale. Namun, citra RGB memiliki tiga kanal, yaitu Merah (R), Hijau (G), dan Biru (B). Untuk mengetahui ukurannya tinggal mengalikan 3 dengan ukuran pikselnya.
-
Floating Points
Citra ini tidak menyimpan ukuran dalam bentuk integer melainkan dalam float atau desimal. Hal ini dikarenakan citra ini menyimpan suatu ukuran tertentu setiap pikselnya. Citra model ini sering ditemukan pada dunia kesehatan seperti citra hasil CT Scan, MRI, atau Ultrasonografi (USG).
-
Latihan
Referensi
[1] Burger, W., & Burge, M. (2009). Principles of Digital Image Processing. Springer London.
[2] Zhu, Q., Mai, J., & Shao, L. (2015). A Fast Single Image Haze Removal Algorithm Using Color Attenuation PriorIEEE Transactions on Image Processing, 24(11), 3522–3533.
[3] Gonzalez, R., & Woods, R. (2002). Digital image processing. Prentice Hall.
[4] Solomon, C., & Breckon, T. (2011). Fundamentals of Digital Image Processing. Wiley-Blackwell.
