Image Enhancement Domain Spasial Graylevel Transformation
Ruang lingkup dalam Peningkatan Citra atau Image Enhancement ada dua, yaitu: Spasial dan Frekuensi. Spasial mencakup semua teknik memanipulasi citra dalam domain spasial bidang citra. Sedangkan frekuensi memanipulasi citra dalam domain frekuensi dengan teknik transformasi Fourier. Pada pembahasan kali ini, materi difokuskan pada ranah domain spasial dan dengan beberapa praktik penerapannya dengan OpenCV.
Daftar Isi:
- Pentingnya Peningkatan Citra
- Prinsip Dasar
- Transformasi Citra Biner
- Transformasi Citra Negatif
- Transformasi Power-law
- Transformasi Logaritmik
- Latihan
- Referensi
Pentingnya Peningkatan Citra
Tujuan utama dari peningkatan citra adalah memperbaiki suatu citra menjadi lebih jelas secara visual sehingga diperoleh informasi yang diinginkan. Syarat utama untuk melakukan ini bahwa informasi yang diingikan ada di dalam citra tersebut. Kita tidak bisa mengada-adakan sesuatu dari sesuatu yang tidak ada. (*Ngomong apa sih?).
Prinsip Dasar
Pada dasarnya, peningkatan citra adalah perubahan citra lama menjadi citra baru dengan bantuan fungsi transformasi tertentu. Anggap saja kita memiliki citra \(f(x,y)\), dengan fungsi transformasi T, maka akan diperoleh citra baru \(g(x,y)\). Perhatikan persamaan berikut:
\[g(x,y) = T[f(x,y)]\]di mana \(x,y\) adalah koordinat titik citra.
Transformasi Citra Biner

Gambar 3.1. (a) Citra grayscale asli. (b) Citra biner dari (a)
Pada pertemuan 2 sudah disebutkan mengenai citra biner. Transformasi menjadi citra biner cukup sederhana, yaitu mengubah nilai intensitas tiap pikselnya menjadi hitam atau putih. Kapan piksel tersebut harus hitam atau putih? Untuk menentukan ini, ada pembeda yang disebut dengan threshold. Threshold ditentukan dengan suatu angka. Sebagai contoh, dengan citra grayscale 8-bit, ditentukan nilai threshold sama dengan 110. Artinya, jika intensitas pada piksel kurang dari 110, maka intensitas pada titik tersebut diubah menjadil nol (0). Dan sebaliknya, jika lebih dari sama dengan 110, intensitas diubah menjadi 255. Besarnya nilai intensitas tiap piksel jika tulis dengan persamaan matematis adalah:
\[t = \left\{ \begin{aligned} 255, && t \ge 110 \\ 0, && t \lt 110 \end{aligned} \right.\]dan \(t\) adalah nilai threshold. Hasilnya seperti pada Gambar 3.1.
Transformasi Citra Negatif

Gambar 3.2. (a) Citra grayscale asli. (b) Citra negatif dari (a)
Citra negatif adalah citra dengan intensitas terbalik dengan citra aslinya. Fungsi ini dirumuskan dengan:
\[g(x,y) = 255 - f(x,y)\]Contoh: pada satu titik piksel dengan intensitas sebesar 90, maka nilai negatifnya adalah \(255 - 90 = 165\). Adapun hasilnya seperti Gambar 3.2.
Tranformasi Power-law
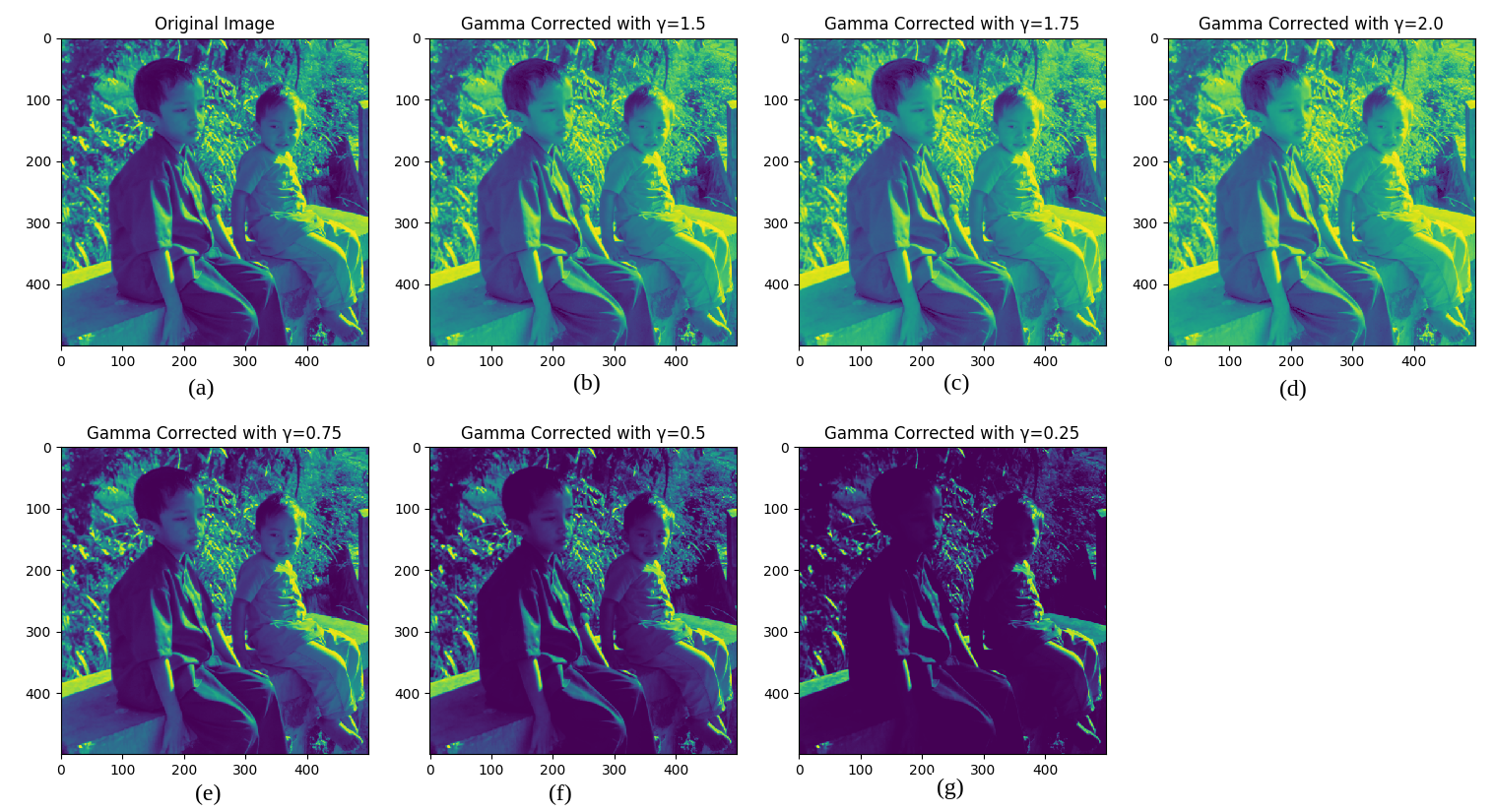
Gambar 3.3. (a) Citra grayscale asli. (b) - (d) adalah citra hasil koreksi gamma dengan nilai \(\gamma = 1.5, \gamma = 1.75\), dan \(\gamma = 2.0\). (d) - (f) adalah citra hasil koreksi gamma dengan nilai \(\gamma = 0.75, \gamma = 0.5\), dan \(\gamma = 0.25\).
Banyak peralatan elektronik yang digunakan untuk pencitraan mengadopsi power-law. Pada kondisi, peralatan ini menangkap luminas dengan baik. Beberapa perangkat display layar monitor juga demikian. Oleh karena itu, diperlukan transformasi untuk mengoreksi luminans. Proses koreksi ini disebut dengan gamma correction. [1][2] Secara umum, fungsi transformasi ini dirumuskan dengan:
\[g(x,y) = Kf(x,y)^\frac{1}{\gamma}\]dengan \(\gamma\) sebagai nilai gamma dan \(K\) adalah konstanta. Hasil dari transformasi gamma bisa dilihat pada Gambar 3.3.
Transformasi Logaritmik
Dampak dari tranformasi logaritmik adalah meningkatkan intensitas piksel-piksel gelap dan mengurangi intensitas piksel yang cerah [1] (lihat Gambar 3.4). Fungsi logaritmik yang digunakan adalah:
\[g(x,y) = c \log(1 + f(x,y))\]di mana \(c\) diperoleh dari:
\[c = \frac{255}{\log[1 + \max(f(x,y))]}\] Gambar 3.4 (a) Citra asli, (b) citra hasil transformasi logaritmik
Gambar 3.4 (a) Citra asli, (b) citra hasil transformasi logaritmik
Latihan
Referensi
[1] Gonzalez, R., & Woods, R. (2002). Digital image processing. Prentice Hall.
[2] Solomon, C., & Breckon, T. (2011). Fundamentals of Digital Image Processing. Wiley-Blackwell.
